Conseil:
On ne peut que conseiller de s’attarder sur le début de la leçon pour bien comprendre les trois éléments: antécédent, image, fonction.
Toutes les erreurs à venir viendront d’un manque de précision dans la compréhension de comment sont reliés ces trois éléments.
Une clé, peut être de se convaincre que l’on n’a pas accès réellement à la fonction mais seulement à la transformation de l’image en antécédent.
Notion de fonction
Définition
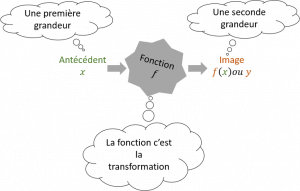
Une fonction est un procédé qui, à un nombre x, fait correspondre un nombre unique appelé image de x
Notation
Par une fonction f, l’image d’un nombre est notée \( f(x) \) (lire « f de x »).
On note:
\( f: x \rightarrow f(x) \)
Notation pour comprendre
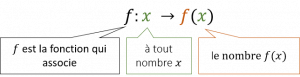
Cette notation permet d’être proche du langage.
C’est celle que l’on privilégie au début dans la rédaction d’un problème.
La phrase type est alors :
« On définit la fonction f qui à tout nombre x associe le nombre f(x) : »
ou
« On définit la fonction f qui associe à tout nombre x le nombre f(x) : »
Notation pour manipuler
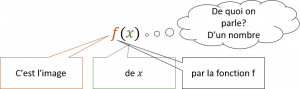
Cette notation utilisée comme ci-dessous:
\( y=f(x) \ ou \ f(x)=2x^2-1 \)
autorise la manipulation de l’image de x; l’égalité permet d’utiliser les « mathématiques », comme les opérations, les équations…
Attention!
C’est celle-ci qui induit en erreur en confondant image et fonction.
Remarque sur « un nombre unique »
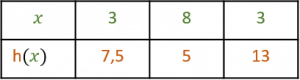 | 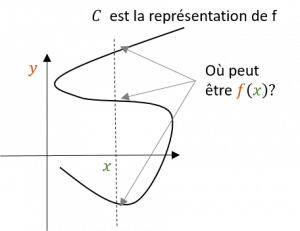 |  |
Un antécédent ne peut avoir qu’une image.
- Si 3kg de pomme valent 7,5€, ils ne peuvent pas valoir en même temps 13€.
- Si x est la distance d’un objet à Pierre, et y est sa hauteur: il ne peut pas être en même temps à trois hauteurs différentes.
- Si un objet est 7 il n’est pas 8.
Déterminer des images et des antécédents
Définition
Si un nombre b a pour image le nombre a par une fonction \( f \), on dit que b est un antécédent de a par la fonction \( f \).
\( f(x)=y \)
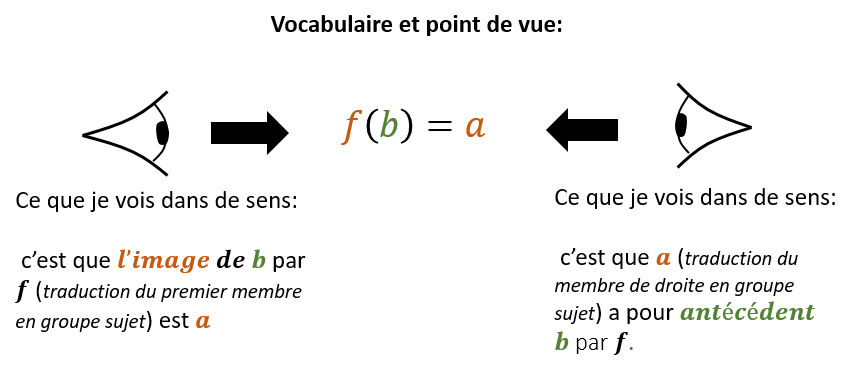
Catégorisation de \( f(a)=b \)
On a deux types de problèmes : trouver a ou trouver b
Exemple avec \( h(x)=6 – \frac{4}{5}x \) et \( g(x)=4x – 9 \)
Trouver un antécédent
Méthode par lecture directe:
C’est ce que l’on utilise dans un tableau ou un graphique (sur un graphique on fait des estimations).
f(6)=9, donc l’antécédent de 9 est 6.
Méthode par résolution de l’équation:
Il faut la représentation par la formule.
\( h(x)=15 \) se lit quel est l’antécédent de 15 ?
On a \( h(x)=6- \frac{4}{5} x=15 \newline -\frac{4}{5} x=15-6=9 \newline x=\frac{9}{\frac{-4}{5}} =9 \times \frac{-5}{4}=\frac{-45}{4} \)
Remarque : La recherche de l’antécédent revient à résoudre une équation.
Il faut faire attention à la division par une fraction qui revient à multiplier par un inverse.
Trouver une image
Méthode par lecture directe:
Avec des représentations graphique ou en tableau
f(6)=9, L’image de 6 est 9.
Méthode par le calcul:
Il faut la représentation par une formule.
\( g(5) \) ?
\(g(x)=4x-9, \newline g(5)=4 \times 5-9 \)
L’image de 5 est 11.
Le piège
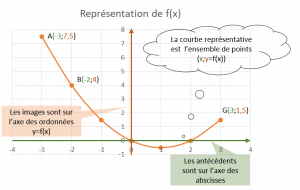
Une grande partie des erreurs proviendront plus tard de la confusion entre la fonction et sa représentation, et en particulier la représentation graphique.
La clé est de se dire qu’une représentation graphique n’est pas autre chose que l’ensemble des couples (x; f(x)), c’est à dire des manifestations de la fonction.
Tracer une représentation graphique d'une fonction
Définition
Dans un repère, la représentation graphique d’une fonction f est l’ensemble des points de coordonnées \( (x;f(x)) \). Cette représentation graphique est également appelée courbe représentative de la fonction f.
Méthode: représentation de la fonction \(f(x)=0,5 x^2 -x \)
| Par la formule | La fonction f est la fonction qui à tout nombre x associe le nombre f(x) : \( x \rightarrow f(x)=0,5 x^2 -x \) | ||||||||||||||||||||||||
| Par le tableau |
Le point B de coordonnées (-2 ; 4) est tel que : \5 f(-2)=4 \° | ||||||||||||||||||||||||
| Par le graphique |
Pour tracer la courbe représentative de f, on place les points qui appartiennent à la courbe représentative de f. |
De nos jours c’est probablement l’une des utilisation majeure des mathématiques dans nos vies quotidienne.
Exploiter la représentation graphique d'une fonction
Méthode
- Pour déterminer graphiquement l’image d’un nombre x, on place x sur l’axe des abscisses et on lit l’ordonnée du point de la courbe correspondant.
- Pour déterminer graphiquement les antécédents d’un nombre y, on place y sur l’axe des ordonnées et on lit les abscisses des points de la courbe correspondants.
Catégorisation de tâches sur un graphique
Trouver l’image de x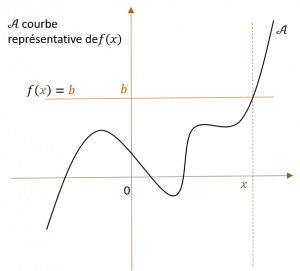 | Trouver un antécédent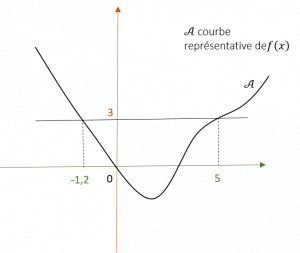 |
Comparer des fonctions: quand \( g(x)\ge f(x) \) | Résoudre une équation \( g(x)=f(x) \)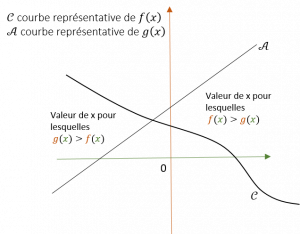 |