Le programme:
Au collège on découvre les fonctions et on étudie plus particulièrement les fonctions affines qui sont de degré 1.
Pourquoi?
Car ce sont les fonctions qui modélisent les situations que l’on doit maitriser à la fin du collège: la proportionnalité.
Au lycée, en seconde on étudie des outils pour décrire les fonctions…
Ensuite chaque année on étudie des fonctions particulières et de nouveaux outils pour les exploiter.
Reconnaitre et utiliser une fonction affine
Définition
m et p désignent deux nombres.
Une fonction affine est une fonction qui, à tout nombre x, associe le nombre \( mx+p \).
Si on désigne par f cette fonction, on peut noter:
\( f : x \rightarrow mx+p \) ou \( f(x)=m(x)+p \)
Propriété
f désigne une fonction
- Si f est une fonction affine, alors sa représentation graphique est une droite.
- Si la représentation graphique de f est une droite, alors f est une fonction affine.
Représentation des fonctions affines
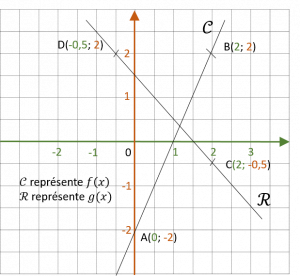
| Par la formule | La fonction f est la fonction qui à tout nombre x associe le nombre f(x) : \( x \rightarrow f(x)=2x-2 \) La fonction g est la fonction qui à tout nombre x associe le nombre g(x) : \( x \rightarrow g(x)=-x+1,5 \) | ||||||||||||
| Par le tableau |
|
||||||||||||
| Par le graphique |
|
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Interpréter les paramètres d'une fonction affine
Définition et propriétés
m et p désignent deux nombres, f désigne la fonction affine \( f : x \rightarrow mx+p \) et \( d \) est sa représentation graphique.
- Le nombre m est appelé coefficient directeur ou pente de la droite \( d \). En restant sur la droite \( d \), si on augmente de 1, alors l’ordonnée augmente de m.
- Le nombre p est appelé ordonnée à l’origine de la droite \( d \).
C’est l’ordonnée du point d’intersection de la droite \( d \) avec l’axe des ordonnées
Trouver l’expression d’une fonction affine à partir du graphique :
\( f(x)=mx+p \)
Fonction croissante \( m > 0 \)
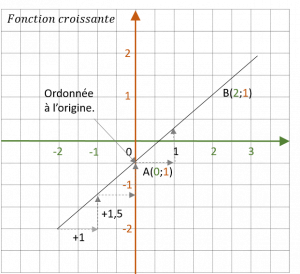
L’ordonnée à l’origine donne le nombre p:
Pour \( x=0 \) on a ( p= -0,5 \)
Quand (\x \) augmente de 1, \(f(x)\) augmente de 1,5.
Coefficient directeur : m=1,5
Fonction décroissante \( m<0 \)
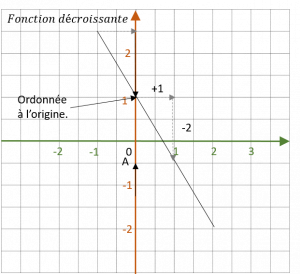
L’ordonnée à l’origine donne le nombre p: \( p = 1 \)
Quand \( x \) augmente de 1, \( f(x) \)diminue de-1
Coefficient directeur : \m = -1 \)
\( f(x) = – x -0,5 \)
C’est la fonction la plus utile car elle modélise la proportionnalité.
Reconnaitre et utiliser une fonction linéaire
Définition
M désigne un nombre. La fonction linéaire de coefficient m est la fonction qui, à tout nombre x, associe le nombre mx, c’est-à-dire le produit de m par x.
Si on désigne par f cette fonction, on peut noter:
\( f : x \rightarrow mx ou f(x)=mx. \)
Propriété
La représentation graphique d’une fonction linéaire de coefficient m est une droite d passant par l’origine du repère. Le nombre m est le coefficient directeur ou la pente de la droite.
Représentation des fonctions linéaires
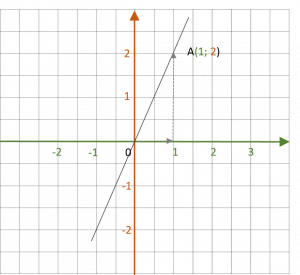
| Par la formule | La fonction f est la fonction qui à tout nombre x associe le nombre f(x) : \( x \rightarrow f(x)=2x \) | ||||||
| Par le tableau |
|
||||||
| Par le graphique |
|
Propriété
Une situation de proportionnalité de coefficient de proportionnalité m peut être traduite par une fonction linéaire de coefficient m.