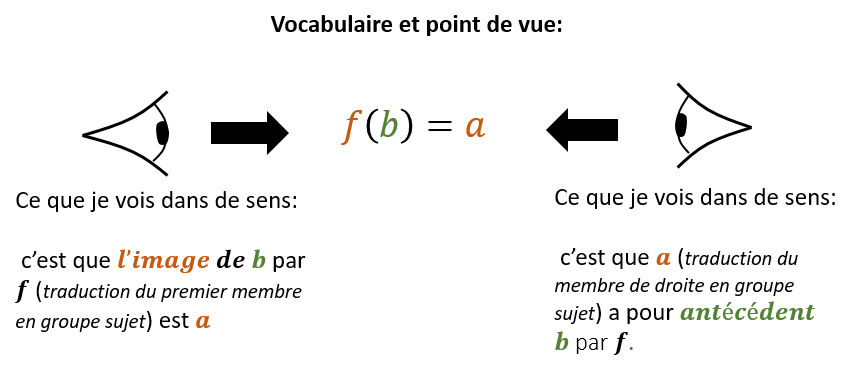La grande question en maths et dans la vie quotidienne, est :
« Peut on calculer une grandeur à partir d’une autre? »
C’est le premier chapitre du domaine qui deviendra le plus important au lycée.
Avertissement:
- Cet objet mathématique très important véhicule un grand nombre d’idées fausses, de confusions, d’imprécisions
- On peut facilement croire que l’on a compris à réussissant les petits exos, mais au fond c’est très flou.
Nombre de cas et taille de la population
Voici les tailles moyennes des hommes et des femmes dans différents pays et le nombre de décès dus au coronavirus au 1er oct. 2021.
| H | F | Décès | |
| All. | 180,3 | 166,2 | 93791 |
| Brésil | 175,7 | 162,4 | 598000 |
| Japon | 170,8 | 158,3 | 17730 |
| R. U. | 137000 | ||
| Australie | 178,8 | 164,7 |
a) Déterminer la tailles des hommes en Angleterre.
b) Déterminer le nombre de décès en Australie.
Pays et nombre de décès
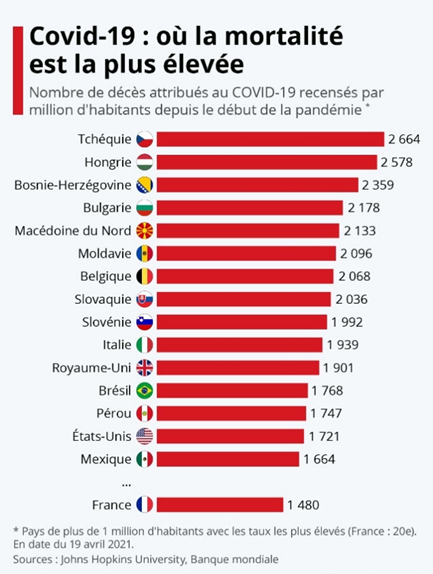
a) Déterminer les deux grandeurs qui décrivent cette situation.
b) Déterminer le nombre de décès par millions d’habitants en Espagne.
Perspectives au début de l’épidémie
Au début de l’épidémie des scientifiques ont cherché à alerter la communauté internationale à partir des premières données chinoises, italiennes et espagnoles.
Le taux de mortalité du virus était de l’ordre de trois pour cent cas constatés. En général, il faut que 70% de la population ait contracté le virus pour que la propagation s’arrête et que le virus devienne inoffensif.
En France il y a à peu près 70 millions d’habitants.
a) Combien de décès pouvaient-ils prévoir si on ne faisait rien ?
b) Quels sont les modèles que supposent de tels calculs ?
Propagation du virus delta
Pendant l’été et la propagation de la variante delta, voici les données que nous pouvions trouver sur internet :
| Durée de contagiosité | 10 jours |
| Nombre moyen de personnes non vaccinées infectées par une personne porteuse non vaccinée | 8 |
a) Considérons une personne infectée non vaccinée le premier juillet. Au bout de 10 jours, elle sera responsable de combien d’infections ? 20 jours, 30 jours, 60 jours ?90 jours ?
b) Comment décrire cette dépendance.
Décès et nombre de cas
Dans ce tableau on trouve le nombre de cas recensé.
| cas (millions) | décès(millier) | ||
| Etats-Unis | 43,6 | 701 | |
| Inde | 33,8 | 449 | |
| Allemagne | 4,26 | 94 | |
| R. U. | 7,87 | 137 | |
| France | 118 | ||
| Espagne | 4,96 | ||
| Canada | 1,64 | 28 |
a) Placer ces points dans un graphique (ordonnée ; décès, abscisse : cas)
b) Que peut-on remarquer ?
c) Quel est le rapport médian entre les décès et le nombre de cas.
d) Compléter le tableau en estimant les valeurs manquantes en supposant que le nombre de cas et le nombre de décès sont proportionnels, et comparer avec des estimations faites à partir du graphique.
e) Comment décrire cette dépendance.
Décès et temps
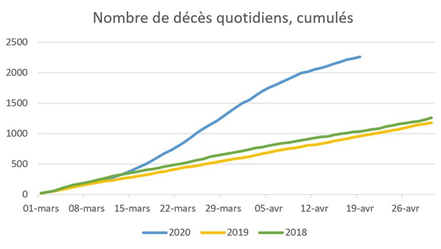
a) Voici la comparaison des courbes de décès au début des années 2018, 2019, 2020. Que pouvez-vous en déduire.
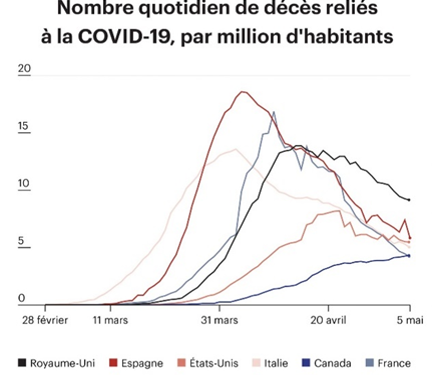
a) Imaginons nous vers le 20 mars. Que pouvait-on prévoir si on ne faisait rien ?
Prenons par exemple la courbe de l’Espagne.
b) Qu’ont permis les différents confinements.
Correction
0. Introduction
Après le théorème de Thalès, sa réciproque, triangles semblables et homothétie, la seconde grande partie du programme est la notion de fonction.
La grande question de Thalès était la construction du pont entre la géométrie et le numérique.
La grande question à laquelle doit répondre les mathématiques dans ses applications les plus quotidiennes, et « peut-on calculer une grandeur à partir d’une autre ? ».
Bien sûr que oui, le prix de trois kilo de pommes, un bouquet de roses et d’iris…
L’objet de ce chapitre est d’étudier en profondeur cette question. Elle sera ensuite centrale dans les mathématiques du lycée et universitaires.
Plus que dans n’importe quel autre chapitre, la grande mission des maths aujourd’hui à l’école est la lutte contre les théories complotistes…
Nombre de cas et taille de la population :
On laisse les élèves élaborer leurs arguments. Rappel sur la mission des maths.
Conclusion :
Pour qu’on puisse calculer une grandeur à partir d’une autre il faut qu’elles dépendent l’une de l’autre.
Donc la grande question revient donc d’abord à décrire comment deux grandeurs peuvent dépendre l’une de l’autre.
Pays et nombre de décès
On laisse les élèves élaborer leurs arguments. La grandeur nom n’a pas de projection quantitative. C’est un signifiant et non le signifié. Si on avait des populations alors peut-être que c’est possible.
Conclusion :
Deux grandeurs peuvent être dépendantes l’une de l’autre mais il faut que cette dépendance soit quantitative !
Conclusion des deux premières situations
« Calculer une grandeur à partir d’une autre ? » est d’abord comprendre « comment deux grandeurs dépendent l’une de l’autre ? ».
Perspectives au début de l’épidémie
a) Nombre de personnes infectées : \( 70 \times 0,7=49 \)
Nombre de décès : \( 49 \times 0,03=1,5 \)
1,5 million de morts.
b) Les calculs que l’ont fait, les pourcentages, supposent que les grandeurs que l’on étudie soit proportionnelles.
C’est une dépendance, particulière:
(i) si je prends 0 pour ‘une l’autre est 0.
(ii) si on multiplie l’une par un nombre l’autre aussi.
(iii) l’unité a un sens.
Penser au contre-exemple du poids et de l’âge d’une personne.
Conclusion :
Les grandeurs proportionnelles est le type de dépendance que l’on étudie au collège. On cherche à s’y ramener quand c’est possible. On a différentes représentations : pour calculer, pour comprendre, pour comparer.
Propagation du virus delta
Le rythme de la propagation est le suivant:
8;64;512;262 144;134 217 728
Bien sûr là on le fait avec les élèves. On les accompagne à cette expression complexe.
\( y=8^{t/10} \)
Conclusion :
On peut calculer une grandeur à partir d’une autre même si ce n’est pas du domaine de la proportionnalité. Ces types de dépendance seront étudiés au lycée.
Conclusion des troisième et quatrième situations
Lorsque deux grandeurs sont dépendantes l’une de l’autre on peut chercher à qualifier cette dépendance.
Dès que la dépendance est modélisée mathématiquement, c’est-à-dire, traduite en phrase mathématiques, alors on peut calculer (ou au moins estimer) une grandeur à partir d’une autre.
Décès et nombre de cas
a) Une des tâches essentielles en mathématiques est la représentation des informations. Le graphique est un mode de représentation.
b) On a l’impression d’un alignement. Enlevons comme en statistiques les valeurs extrêmes.
c) \( (13,3 ;16;16,6;17,4 ;17,5 ;22) \Rightarrow \ donc \ 17 \)
d) Qu’est-ce qu’on est en train de faire ?
On modélise une situation.
La proportionnalité est un modèle que l’on maitrise et on essaie de l’appliquer à cette situation. Avons-nous suffisamment d’argument pour le valider ?
e) On décrit cette dépendance par :
\( y=a \times x ; y=17 \times x \)
Conclusion :
La représentation graphique de la dépendance par des nuages de points, permet d’envisager un modèle qui permet alors d’interpoler.
Les trois modes de représentation d’une même réalité, la dépendance : le tableau, le graphique, la formule.
Décès et temps
a) Le nombre de décès et la durée sont normalement proportionnels.
On voit qu’en 2020, la proportionnalité a été rompue. Plaçons nous au 20 mars et extrapolons alors la droite.
Discussion sur la proportionnalité, comparaison ; zone de proportionnalité, extrapoler un comportement proportionnel.
X nombre de décès par jour, t nombre de jour, n nombre de décès dans le mois.
\( n=t \times x \)
Discussion sur les graphiques pour amener les élèves à voir que c’est un outil d’extrapolation, d’interpolation, de prédiction, d’estimation, de comparaison.
Conclusion :
La courbe qui est la représentation graphique d’une dépendance est d’une grande efficacité pour extrapoler, interpoler, comparer.
Conclusion des cinquième et sixième situations
Pour déterminer une quantité à partir d’une autre, il faut pouvoir mettre en évidence, décrire la dépendance de deux quantités.
Cette grande question sera centrale au lycée et vous apprendrez à qualifier et comprendre de nombreux types de dépendance.
Conclusion de l’activité
Au collège, l’objectif est de bien comprendre la plus fréquente des dépendances, celle qui est liée aux situations de proportionnalité.
La dépendance de deux grandeurs est définie par l’objet mathématique « fonction ».
L’une des difficultés sera de ne pas confondre l’objet, la dépendance, avec ses représentations :
-Le tableau
-Le graphique
-La formule
Vocabulaire et définition.
Une fonction est le procédé qui à un nombre x fait correspondre un nombre unique appelé image de x.
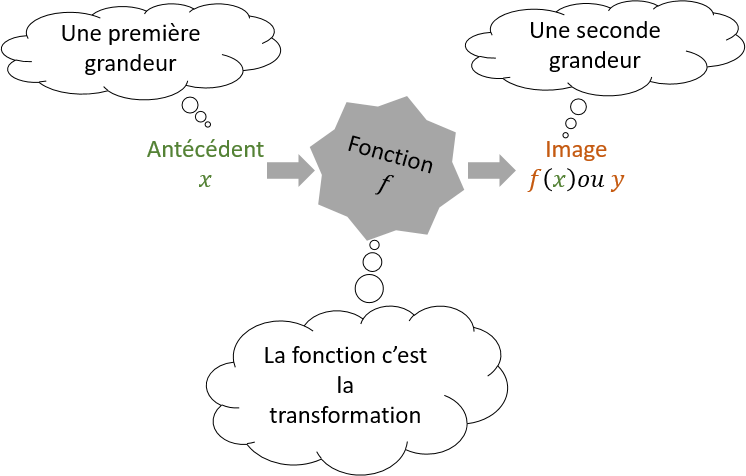
Interprétation par les trois représentations
Un antécédent ne peut avoir deux images! Quelle valeur prendre? | 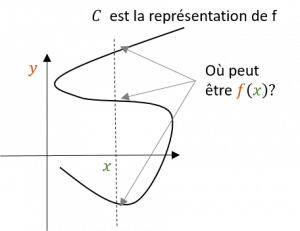 | \( f(x)=8 \newline f(x)=7 \) Donc 8=7, impossible! |
Aide pour fixer le vocabulaire: