A quoi ça sert? Si je reconnais des triangles égaux alors ce que je sais sur l’un est vrai pour l’autre.
– Connaître le vocabulaire : homologue, adjacent – connaître les 3 critères – Avoir compris que l’égalité en géométrie est la « superposition ». | – Utiliser les trois critères – Satisfaire les conditions d’utilisation des différents critères. -Etre capable de rédiger l’utilisation des trois cas. |
Egalité en géométrie
Définition
Deux figures peuvent être dites égales si elles sont superposables.
Les objets (sommets, angles, côtés) superposables sont dits homologues.
Exemple
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Exemple : Les triangles ACB et PQR sont superposables. Le sommet R et C sont homologues. Les segments [QP] et [AB] sont homologues. Les angles \( \hat{A} \ et \ \hat{Q} \) sont homologues | 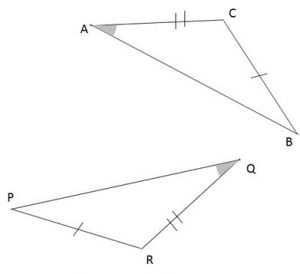 |
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Premier cas d'égalité
Premier cas d’égalité.
Si deux triangles ont un côté de même longueur et des angles adjacents à ce côté deux à deux de même mesure, alors ces deux triangles sont égaux.
| Situer: Dans les triangles ACB et EDF: | 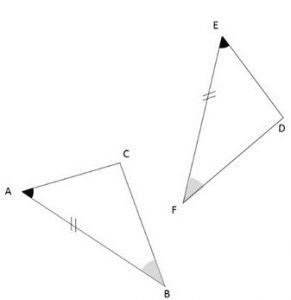 |
Condition: AB=EF \( \hat{A}=\hat{E} et \hat{B}=\hat{F} \)
| |
Propriété: Les triangles ACB et EDF ont un côté de même longueur et des angles adjacents à ce côté deux à deux de même mesure, | |
| Conclusion: donc ils sont égaux. |
Deuxième cas d'égalité:
Deuxième cas d’égalité.
Si deux triangles ont un angle de même mesure compris entre des côtés deux à deux de même longueur, alors ces deux triangles sont égaux.
| Situer: Dans les triangles ACB et EDF: | 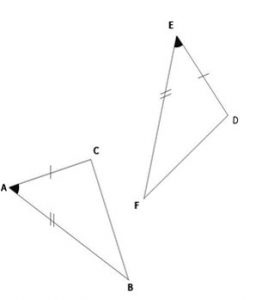 |
|
Condition: \( \hat{A}=\hat{E} \) |
|
|
Propriété: Les triangles ACB et EDF ont un angle de même mesure compris entre des côtés deux à deux de même longueur, |
|
| Conclusion: donc ils sont égaux. |
Troisième cas d'égalité
Définition
Si deux triangles ont ont leurs trois côtés deux à deux de même longueur alors ces deux triangles sont égaux.
| Situer: Dans les triangles ACB et EDF: | 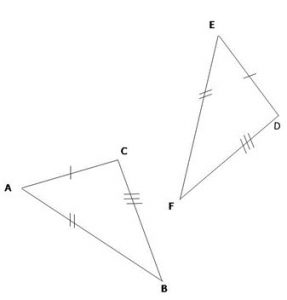 |
Condition: AB=EF | |
Propriété: Les triangles ACB et EDF ont leurs côtés deux à deux de même longueur, | |
| Conclusion: donc ils sont égaux. |