C’est un chapitre difficile pour la rédaction et également car c’est le premier du collège essentiellement basé sur la justification des conclusions.
L’objectif est de bien maitrisé le conditions-conclusion.
- Reconnaitre des triangles égaux
Clé: Il faut connaitre les trois motifs correspondant aux trois cas par cœur.
 |  |  |
| Un côté de même longueur entre deux angles de même mesure | Un angle de même mesure compris entre deux côtés de même longueur | Trois côtés de même longueur. |
Intérêt: Le calcul de longueurs et d’angles sans instruments de mesure représente la catégorie majeure des problèmes de la géométrie.
Méthode:
1) Identifier les trois informations que l’on a dans un triangles.
2) Apparier ces informations avec un autre triangle. Déterminer si c’est un cas où on peut conclure.
3) Si c’est possible, alors les triangles sont égaux.
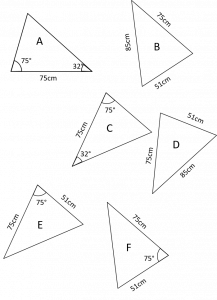
Intérêt
Reconnaitre des triangles égaux est la première étape. C’est l’équivalent de la lecture en français. On doit pouvoir lire les motifs.
MéthodeVoir ci-dessus.
Correction:
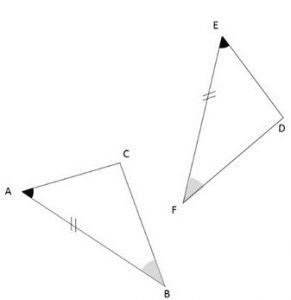
A-C: un côté de même longueur compris entre deux angles de même mesure.
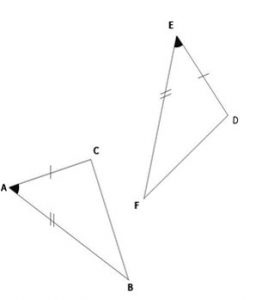
B-D: les trois côtés de même longueur.
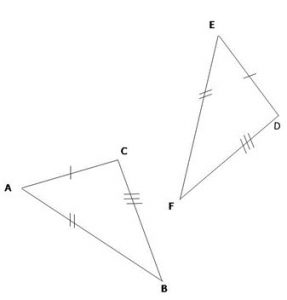
E-F: un angle de même mesure compris entre deux côtés de même longueur.
Identifier les côtés et sommets homologues.
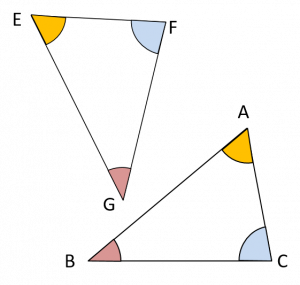
Compléter le tableau.
| Sommets homologues | Côtés homologues | Angles homologues |
| A et … | [AB] et | \( \widehat{BAC} \ et \ … \) |
| B et … | [AC] et | \( \widehat{ACB} \ et \ … \) |
| C et … | [CB] et | \( \widehat{CBA} \ et \ … \) |
Intérêt
Comme tout langage les maths doivent avoir des mots pour nommer les choses. En français vous « sujet », « adjectif », ….
Première méthode:
On reconnait les objets homologues par analogie. « Qui joue le rôle de qui? »
Deuxième méthode:
Si on est habile pour se représenter les déplacements « dans la tête », on peut faire glisser, tourner ou renverser une figure pour la superposer à l’autre.
Les éléments superposables sont les éléments homologues.
Correction
| Sommets homologues | Côtés homologues | Angles homologues |
| A et E | [AB] et [EG] | \( \widehat{BAC} \ et \ \widehat{GEF} \) |
| B et G | [AC] et [EF] | \( \widehat{ACB} \ et \ \widehat{EFG} \) |
| C et F | [CB] et [FG] | \( \widehat{CBA} \ et \ \widehat{EGF} \) |
- Identifier des triangles égaux
Clé: Lire une configuration géométrique
Intérêt: Identifier des triangles égaux ouvre la voix aux calculs de longueurs et d’angles
Méthode:
Lire la configuration avec les motifs disponibles.
Lorsqu’on repère un triangle, on identifie le jeu de donnée et on essaie de l’apparier à un autre.
Si il manque une information alors il faut la chercher.
Rappel sur les angles
On n’a pas beaucoup d’outils avec les angles. Les motifs que l’on peut activer sont:
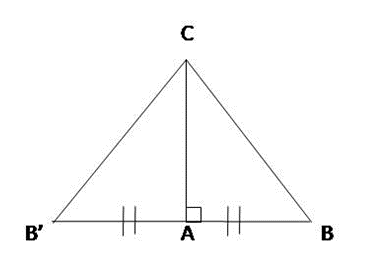
Construire un triangle ABC rectangle en A.
Construire B’, l’image de B par rapport à la symétrie de centre A.
Montrer que le triangle CBB’ est isocèle.
Intérêt
Les différents triangles isocèle et rectangle (et aussi équilatéral) sont à maitriser sous toutes leurs formes. En effet, tout polygone peut se décomposer en triangles.
Méthode: « Se donner une stratégie »
1) Voir les données que l’on a et celles dont on aurait besoin pour satisfaire au but
2) A l’aide des propriétés sur les figures, voir ce qui semble pouvoir être démontré (motif)
=> Choisir une stratégie
-> Quel cas ?
-> Quel côté ? Quel angle ?
3) Etablir les conditions pour pouvoir appliquer un des trois cas
4) Appliquer un des trois cas
Correction
( On traduit la question pour que cela nous donne un but. Isocèle ne nous fait rien faire! Mais dire que les angles en B ou B’ sont égaux ou dire CB est égal à CB’ nous donnent un but.
J’ai choisi d’utiliser le cas d’un angle compris entre deux longueurs car on a presque toutes les informations)
La difficulté majeure de ce chapitre est la rédaction. On développe ici la rédaction en explicitant pourquoi.
| Montrons que BC=B’C | Le but. J’annonce ce que je veux faire |
| A, B, B’ sont alignés par construction donc \( \widehat{B’AC} \) est droit puisque \( \widehat{BAC} \) l’est. | Les conditions. Je me donne la condition qui me manque |
| Dans les triangles ACB’ et ACB, on a: | Où? Je m’installe dans les triangles dans lesquels je veux travailler |
\( AB=AB’; AC=AC; \widehat{BAC}=\widehat{B’AC} \) On est dans le cas d’un angle de même mesure compris entre deux côtés de même longueurs, les triangles ACB’ et ACB sont donc égaux. | Les informations + la propriété=> conclusion. Nous allons considérer que ce type de rédaction est suffisant: j’énonce le motif (l’un des trois cas) et je conclue. |
| Les côtés homologues CB’ et CB sont donc égaux, le triangles est isocèle en C. | Conclusion. En rapport au but que je me suis donné au départ |
ABC est un triangle isocèle en A tel que AC=AB=5cm et BC=4cm.
M et N sont les milieux respectifs de [AC] et [AB].
a) Construire la figure.
b) Montrer que ABM et ACN sont égaux.
c) Montrer que BMC et CNB sont égaux.
Intérêt
Un autre problème dans un triangle isocèle avec les milieux des côtés égaux. Cette configuration sera à la source de Thalès en 3ème.
Méthode
Voir ci-dessus.
Correction.
b) ( On traduit la question pour que cela nous donne un but. Montrer qu’ils sont égaux ne nous fait rien faire! Mais choisir un des trois cas va pouvoir nous indiquer ce qu’il faut faire.
J’ai choisi d’utiliser le cas d’un angle compris entre deux longueurs car on a toutes les informations)
| Montrons que AMC=ANC | Le but. J’annonce ce que je veux faire |
| Les conditions. Je me donne la condition qui me manque | |
| Dans les triangles AMB et ANC, on a: | Où? Je m’installe dans les triangles dans lesquels je veux travailler |
\( AM=AN \), par construction: M et N milieux de segments de même longueur AC=AB. \( \widehat{MAB}=\widehat{NAC} \) On est dans le cas d’un angle de même mesure compris entre deux côtés de même longueurs, les triangles AMB et ANC sont donc égaux. | Les informations + la propriété=> conclusion. Prendre le temps de justifier les conditions. |
| Elle est donné au-dessus. | Conclusion. En rapport au but que je me suis donné au départ |
c) Montrons que MBC=NBC
ANC et AMB sont égaux donc les côtés homologues le sont, NC=MB.
Dans les triangles MBC et NBC, on a:
MB=NC; MC=NB (par construction; BC=BC
On est donc dans le cas où deux triangles ont leur trois côtés de même longueur, donc MBC et NBC sont égaux.

- Utiliser les triangles égaux
Clé: Lire une configuration géométrique
Intérêt: Identifier des triangles égaux ouvre la voix aux calculs de longueurs et d’angles
Méthode:
Identifier des triangles égaux permet de déduire les longueurs ou angles d’objets homologues et donc de montrer des propriétés ou calculer.
ABC est un triangle rectangle isocèle en A tel que AB=AC=6cm.
I est le milieu de BC.
On place les points M sur [AC] et N sur [AB] tel que AM=AC=2.

a) Montrer que \(\widehat{IBA} = \widehat{IAC} \)
b) Montrer que IAM et IBN sont égaux.
c) En déduire la nature du triangle MIN.
Intérêt
On travaille encore dans le triangle isocèle. Vous devez sentir l’importance de l’expérience dans une configuration. C’est cette expérience qui donne de l’assurance.
Méthode
On lit la configuration en ayant en tête l’objectif.
On tente de trouver intuitivement ce qu’il faut faire pour se donner des sous-buts.
Ensuite on essaie de démontrer que nos hypothèses sont justes.
Correction
( L’objectif est de montrer que AMI et INB sont égaux.
La lecture de la première question nous indique que l’on va chercher à appliquer le cas d’un angle compris entre deux longueurs.)
a) (Intuitivement on voit d’une part, que AI partage l’angle en deux, donc on devrait avoir \( \widehat{IAC}=45° \) , la moitié de l’angle droit. Mais on va devoir le montrer. (Ce sera un résultat que vous pourrez utiliser, la médiane relative à l’hypoténuse d’un triangle rectangle isocèle est aussi médiatrice et hauteur). D’autre part, ACB est rectangle isocèle dont l’angle à la base est 45°. C’est ce que l’on veut.
On a donc notre stratégie. )
a) \( \widehat{(ABI}= \widehat{ACI}=45° \) car le triangle ABC est rectangle isocèle en A.
Dans les triangles ACI et AIB, on a aussi:
CI=IB par construction; AC=AB par nature.
Les triangles ABI et ACI ont un angle de même mesure compris entre des côtés de même longueur donc ils sont égaux.
Les angles homologues sont égaux: \( \widehat{MAI}=\widehat{ IAB} \).
\( \widehat{CAB}=90°, donc \widehat{MAI}=45° \)
On a donc \( \widehat{MAI}=\widehat{ ABI}=45° \)
b) On veut montrer que IAM et IBN sont égaux.
Dans les triangles MAI et INB, on a:
\( \widehat{MAI}=\widehat{ ABI}; AI=AI; AM=NB \)
Les triangles CNI et AMI ont un angle de même mesure compris entre des côtés de même longueur donc ils sont égaux.
c) Les côtés homologues MI et IN sont égaux.
Le triangle MNI est isocèle.
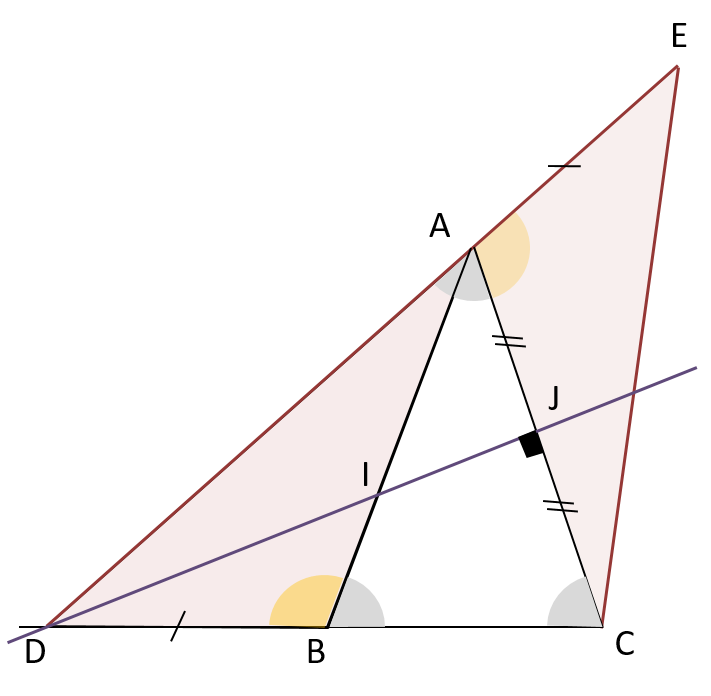
ABC est un triangle isocèle en A. La médiatrice de AC coupe (BC) en D.
On construit E sur la droite (DA) tel que AE=BD.
a) Démontrer que les triangles ABD et ACE sont égaux.
b) En déduire que le triangle CDE est isocèle.
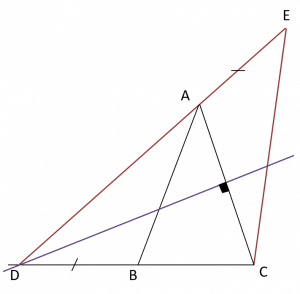
Intérêt
L’intérêt de cet exercice est la difficulté de se donner un but pour commencer.
La disposition est telle que l’on a du mal à trouver quel cas il faut chercher, comment satisfaire les conditions.
Normalement vous aller essayer de nombreuses pistes.
Méthode
C’est quelque chose qui est difficile. C’est reconnaitre les situations d’impasse. J’avance dans une direction et je vois que je ne peux plus rien faire. Alors il faut savoir revenir en arrière et même parfois au début.
Correction:
(Il faut lire la figure: on a commencé par coder le triangle isocèle, puis D appartient à la médiatrice donc DAC est isocèle en D, on code les angles.
On aperçoit le cas d’un angle coder en jaune compris entre deux côtés de même longueur.
On se donne le but de montrer que les angles en jaune sont égaux.)
Les angles \( \widehat{DBC} \) et \( \widehat{DAE} \) sont plats.
On a D qui appartient à la médiatrice de [AC] et ABC isocèle en A, donc:
\( \widehat{CAD} =\widehat{CBA} \)
\( \widehat{DBA} = 180 – \widehat{CAD} \newline \widehat{EAC} = 180 – \widehat{CAD} \)
Comme \( \widehat{CAD} =\widehat{CBA} \), alors \( \widehat{DBA} =\widehat{EAC} \)
Montrons que DBA et AEC sont égaux.
Dans les triangles DBA et AEC, on a:
AE=BD par construction; AB=AC par nature, triangle isocèle; \( \widehat{DBA} =\widehat{EAC} \)
Les triangles ABD et ACE ont un angle de même mesure compris entre des côtés deux à deux de même longueur donc ils sont égaux.
b) Les angles homologues en D et E sont égaux, donc le triangle CDE est isocèle.