La manipulation des nombres entiers ne pose pas de problèmes pour les additions, les soustractions et les multiplications. En effet les sommes, différences ou produits sont des nombres entiers.
Mais qu’en est-il lors du partage de deux nombres entiers et que l’on souhaite une réponse entière?
Le platane de Lamanon

C’est un très vieux platane, on dit qu’il a été planté au XVI siècle par Catherine de Médicis venue rendre visite à Nostradamus.
Il mesure 27 m de haut.
C’est difficile de se rendre compte de sa hauteur.
On pourrait comparer avec immeuble. Les étages d’immeubles anciens ont 4 m de hauteur environ et ceux des immeubles plus récents 3 m de hauteur.
L’objectif de la situation:
Amener l’élève à produire un schéma (reproduction des étages à côté de l’arbre) pour repérer la répétition du diviseur.
C’est en effet la situation élémentaire de comparaison « fois plus et fois moins ».
Cette situation à trois éléments: un élément à mesurer, un élément qui joue le rôle d’unité, et le nombre de répétition qui est une mesure du premier élément.
Ce sera l’image mentale pour les multiples et diviseurs et comprendre le reste.
On cherche le nombre d’étages d’un immeuble équivalent en hauteur au platane :
\( 27 = 9 \times 3 \) ou \(27 = 6 \times 4 + 3 \)
Le platane est haut comme un immeuble de 9 étages de 3m ou un peu plus de 6 étages de 4m.
Cette expression numérique très particulière a un nom :
Bilan : Division euclidienne.
La division euclidienne permet d’écrire un nombre entier sous la forme d’un produit de deux nombres entiers et d’un reste entier inférieur au diviseur.
\( dividende \ = diviseur \ \times \ quotient \ + \ reste \) avec reste < diviseur
$$ a \times b + q \ , \ avec \ r<b $$
Les monuments

Comparons la hauteur de ces monuments parisiens.
a) A combien d’Arc de triomphe superposés les tours Eiffel et Montparnasse sont-elles équivalentes?
A combien de Notre Dame superposées ?
Tour Montparnasse: 210 m
Tour Eiffel: 324 m
Arc de Triomphe: 50 m
Notre Dame: 69 m
** supplémentaire
b) Ces deux tours sont équivalentes à des immeubles de combien d’étages de 3m ou 4m?
a) C’est comme si on mesurait la hauteur de la tour Montparnasse avec une unité équivalent à la hauteur de l’arc de Triomphe (ADT). (on recommande de faire la schéma).
\( 210 =4 \times 50 + 10 \). La tour M. mesure un peu plus de 4 ADT.
\( 324 = 6 \times 50 + 24 \). La tour E. mesure un peu plus de 6 ADT.
En prenant maintenant comme unité Notre Dame (ND).
\( 210 =3 \times 69 + 3 \). La tour M. mesure un peu moins de 4 ND.
\( 324 = 4 \times 69 + 48 \). La tour E. mesure entre 4 et R ND.
b) \( 210 = 3 \times 70 \) A un immeuble de 70 étages de 3m.
\( 210 = 4 \times 52 \) A un immeuble de 52 étages de 4m.
\( 324 = 3 \times 108 \) A un immeuble de 108 étages de 3m.
\( 324 = 4 \times 81 \) A un immeuble de 81 étages de 4m.
Bilan : multiples et diviseurs, cas où le reste est nul.
Lorsque le reste de la division euclidienne est nul on parle de multiples et diviseurs. Observer que l’on exprime un nombre par un produit: \( a = b \times q \)
Vocabulaire
On a trois mots pour décrire cette phrase mathématique:
- je mets a en groupe sujet:
a est un multiple de b ou a est divisible par b
- je met b en groupe sujet:
b est un diviseur de a
Pour trouver des multiples ou diviseurs je vérifie que \( \frac{a}{b} \) est entier.
La fête foraine

Lula et Nawal vont à la fête foraine. Les lumières du bateau, de la boule et du bras articulé apparaissent pendant 1s vertes en même temps !
« – Je te parie 10€ que dans une 1min les lumières des trois manèges sont à nouveau vertes ! Dit Lula.
– Impossible, lui répond Nawal. »
Lula a observé que les lumières de chaque manège changent chaque seconde de couleur. L’ordre des couleur est pour:
Le bateau : Vert ; Rouge ; bleu
La boule : Vert ; Bleu ; Blanc; jaune
Le bras articulé : Vert ; Rouge ; Bleu ; Jaune ; Blanc ;
La situation
De quoi on parle? Trois manèges dont les lumières changent de couleur.
Les lumières changent de couleur dans un ordre précis et ce n’est pas le même pour chaque manège.
Ce qu’on cherche? Quand on aura trois lumières vertes.
Informations. L’ordre des lumières de chaque manège.
Traduisons l’observation de Lula par un schéma.
Toutes les 3s la lumière du bateau est verte, toutes les 4s celle de la boule est verte et toutes 5s celle du bras est verte.
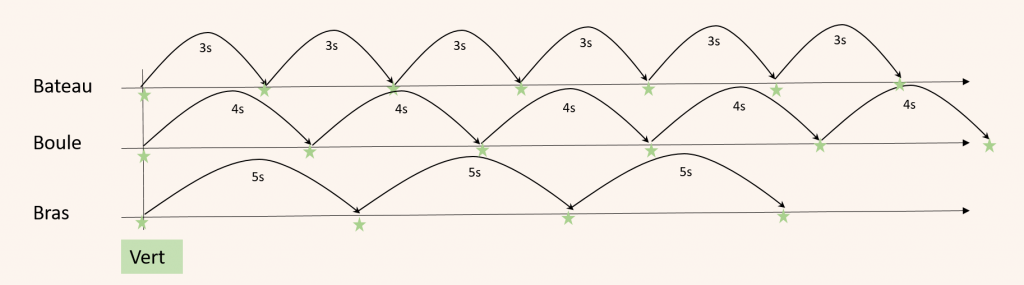
Si on reproduit les cycles on s’aperçoit que à 12s, le bateau et la boule ont une lumière verte en même temps.
Au bout de 15 seconde ce sera la bateau et le bras.
En effet:
\( 12 = 3 \times 4 \). C’est un multiple de 3 et 4, donc au bout de 12 seconde les lumières des deux manèges ont fait des cycles complets.
Le temps t au bout duquel les trois lumières sont vertes en même temps doit être un multiple de 3, 4 et 5.
\( t= 3 \times 4 \times 5 = 60 \)
Donc au bout de 60s les trois lumières seront vertes.