La troisième a pour objectif l’étude des fonctions de degré 1 et 0.
- Les salles de sport à Aix: que choisir?
Pierre aménage à Aix pour une durée de 18 mois. Il veut continuer son activité physique dans une salle de sport et regarde sur internet les offres des trois premiers sites. Son seul souhait est de payer le moins possible. Quelle salle et formule doit-il choisir ?
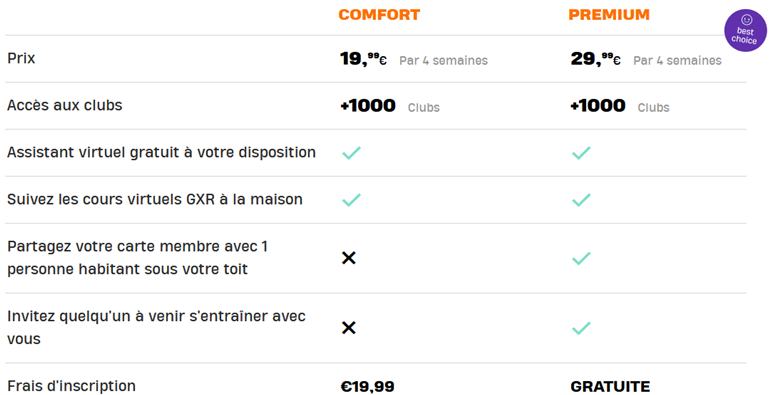
Attention pour la salle Basic Fit:
Le prix n’est pas par mois mais toutes les 4 semaines (dans une année on semaines). Pour pouvoir comparer avec les autres formules, on calcule les prix par mois :
Comfort: \( 19,99 \times \frac{13}{12} = 21,7 €/mois \)
Premium:\( 29,99 \times \frac{13}{12} = 32,5 €/mois \)

Correction
Les grandeurs qui caractérisent cette situation, sont le nombre de mois où Pierre prendra un abonnement et le coût de chaque formule.
Nous allons commencer par Keep Cool, car les formules de Basic-fit ne sont pas en mois et donc ce sera un peu plus compliqué.
A. Représentation sous forme d’un tableau:
- Basic-fit
Les forfaits de cette salle sont calculés par « 4 semaines » alors que les autres sont « en mois ». On doit convertir ces tarifs en prix par mois.
Dans une année il y a 12 mois, et 13 fois 4 semaines.
Pour pouvoir comparer avec les autres formules il nous faut le prix par mois M, donc sur une année \(12 \times M \).
On appelle P le prix payé par 4 semaines, donc sur une année : \( P \times 13 \)
On a donc, \( P \times 13 = 12 \times \times M \Rightarrow M= \frac{13}{12} P \)
Complétons le tableau :
Formule comfort :
Formule Premium : On remarque la situation de proportionnalité
| en € | 0 mois | 3 mois | 6 mois | 12 mois | 18 mois |
| Basic-Fit: Comfort | 19,9 | \( 19,9+3 \times 21,7 = 85\) | \( 19,9+6 \times \newline 21,7 = 149,9\) | 279,9 | 409,9 |
| Basic-Fit: Premium | 0 | \( 3 \times 32,5 = 97,5\) | 194,9 | 389,9 | 584,8 |
Remarquer que la formule Comfort n’est pas proportionnelle ! Si je double le nombre de mois, je ne double pas le prix. Pourquoi ? Observer le rôle de la constante qui est l’abonnement.
- KeepCool
La formule Family ne l’intéresse pas.
Formule premium:
| en € | 0 mois | 3 mois | 6 mois | 12 mois | 18 mois |
| KeepCool: Premium | 39,9 | \( 39,9 +9,9 \times 3= 68,7\) | \( 68,7 + 29,9 \times \newline (6-3) = 158,4\) | \( 68,7+29,9 \times \newline (12-3)=337,8 | 517,2 |
Pour 12 mois : on paie les trois premiers mois à : 68,7€, puis les autres mois à 29,99€.
L’objectif ici est de laisser les élèves calculer, s’approprier la situation.
N’oublions pas les deux grandes questions qui structurent le chapitre.
On est bien en train de calculer une grandeur à partir d’une autre, et nous ne sommes pas en train d’utiliser des propriétés du tableau comme dans des tableaux de proportionnalité. Ce n’est pas de la proportionnalité.
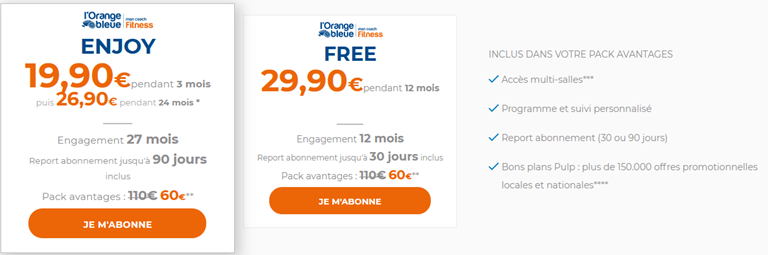
- Orange Bleue
Formule free :
C’est un engagement sur 12 mois. Donc quoiqu’il arrive on paie les 12 mois, soit :
\( 12 \times 29,9=358,8€ \).
Puis au début de la seconde année :
\( 2 \times 358,8=717,6€ \).
Formule Enjoy :
C’est un engagement sur 27 mois.
Donc \( 3 \times 19,9+ 24 \times 26,9=705,3€ \).
| en € | 0 mois | 3 mois | 6 mois | 12 mois | 18 mois |
| Orange Bleue: Enjoy | 705,3 | 705,3 | 705,3 | 705,3 | 705,3 |
Orange Bleue: Free/td> | 358,8 | 358,8 | 358,8 | 7,7,6 | 717,6 |
Bilan.
On peut représenter les fonctions sous forme de tableau.
Le tableau peut être « opérationnalisé » uniquement pour des dépendances de proportionnalité.
Les calculs sont faits en exécutant les « programmes de calcul ».
Si on peut répondre à la question, la comparaison n’est pas aisée.
Pour comparer, la représentation la plus aisée est la graphique.
B. Représentation graphique
On trace les différentes représentations.
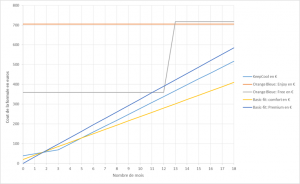
On encourage les élèves à tracer tous les points. Les laisser découvrir les discontinuités.
On pose des questions du type pendant le tracé: quelle formule pour 500€ ?combien de mois pour … ?… Insister sur le fait que le graphique est « opérationnalisable » mais il ne donne qu’une estimation.
Faire les premières interprétations niveau 4ème .
-Reconnaitre la représentation de la proportionnalité : droite qui passe par l’origine.
-Reconnaitre la constante.
On laisse le temps de faire les comparaisons. Et on insiste sur le fait que comparer est une opération ! Vous êtes en train de regarder la différence entre une fonction et une autre.
Une fois que tout le monde a suffisamment avancé.
Nous allons explorer la troisième représentation par la formule.
C. Représentation par une formule
On fait la situation de proportionnalité ensemble, puis on laisse les élèves chercher les formules représentant les constantes.
- BasicFit Premium :
La dépendance du prix par la formule «BasicFit Premium » en € et du nombre de mois peut être modélisée par la fonction qui à tout nombre de mois x associe le prix en € :
\( f: x \rightarrow f(x)=31,5 \times x \)
C’est la définition de la proportionnalité.
On obtient une grandeur en multipliant l’autre par un même nombre, le coefficient de proportionnalité.
On peut donc modéliser la proportionnalité par la fonction :
\( f(x)=ax \), avec a le coefficient de proportionnalité différent de 0.
On appelle ce type de fonction, des fonctions linéaires (droite qui passe par l’origine de coefficient a.
- Orange Bleue : Enjoy
On définit la fonction E qui associe à tout nombre de mois x le prix par la formule «Orange bleue : Enjoy» en €.
Le prix est constant. Il ne dépend pas de x. 705,3 a tout x comme antécédent, ou alors tout x a 705,3 comme image :
\( E: x \rightarrow E(x)=705,3 \)
On appelle ce type de fonction, des fonctions constantes. Elles sont représentées par des droites parallèles à l’axe des abscisses.
- Orange bleue : free
On définit la fonction R qui associe à tout nombre de mois x le prix par la formule «Orange bleue : free » en €.
\( R: x \begin{cases} \rightarrow R(x)=358,8, pour x \in [0;12] \newline
\rightarrow R(x)=717,6 pour x>12 \end{cases} \)
Une fonction peut être définie en plusieurs « morceaux ».
Discuter de la ligne qui relie les points sans trop rentrer dans les détails.
- BasicFit Confort :
On définit la fonction C qui associe à tout nombre de mois x le prix par la formule « BasicFit Comfort » en €.
\( x \rightarrow C(x)=21,7x+19,9 \)
Quelle est l’image de 0 ? C(0)=19,9.
L’image de 0 est ce qu’on appelle l’ordonnée à l’origine. C’est la partie constante de la fonction.
Imaginons qu’on enlève cette partie constante, il resterait \( 21,7 x \) qui est la partie « proportionnelle » de la fonction.
On appelle ce type de fonction, les fonctions affines. Elles sont de la forme :
\( f(x)=ax+b \)
Elles sont représentées par une droite qui coupe l’axe des ordonnées en b, b étant la partie constante de la fonction.
Le coefficient multiplicatif devant a est appelé le coefficient directeur : c’est lui qui va donner la pente de la droite exactement comme dans la situation de proportionnalité.
- KeepCool (Hors programme)
On observe deux parties. La première pour \( x \in [0;3] \).
Cette partie-là peut être modélisée par une fonction affine. L’ordonnée à l’origine est 39. Donc le coefficient constant est 39.
Le coefficient est 9,9. On peut donc écrire la fonction: \( K(x)=9,9x+39 \)
La seconde partie. \( O(x)=K(3)+29,9(x-3) \)

Conclusion
On peut catégoriser les fonctions du premier degré et de degré 0 en trois catégories :
*Les fonctions constantes : \( f(x)=b \)
*Les fonctions linéaires :\( f(x)=a \times x \)
*Les fonctions affines :\( f(x)=a \times x + b \)
Ce sont tous les types de fonctions possibles de degré 1 ou 0.
Nous étudierons maintenant séparément les fonctions linéaires et les fonctions affines.
Pour chacune d’entre elles on construira les procédures pour résoudre les différents problèmes.