Au collège on étudie les fonctions du premiers degré.
Etudier une fonctions signifie:
-être capable de trouver des antécédents et images
-être capable de déterminer la formule
- Fonctions linéaires
Clé: C’est la proportionnalité
Intérêt: On peut difficilement vivre dans le monde sans maitriser la proportionnalité: pour les courses, pour se soigner, pour son salaire…
Méthode:
Connaitre le motif par coeur: \( f(x)=ax \)
Donc trois types de tâche: image, antécédent, coefficient directeur.
a) Déterminer l’expression de la fonction linéaire f sachant que l’image de 3 est 1/2.
b) Déterminer l’expression de la fonction linéaire g :
| x | 7 |
| g(x) | 9 |
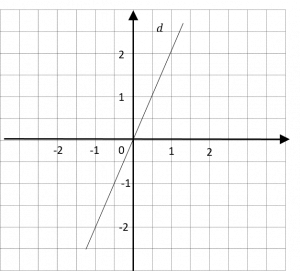
c) Déterminer l’expression de la fonction k dont la représentation graphique est la droite d.
Intérêt
Déterminer l’expression d’une fonction linéaire à partir:
- d’un couple antécédent-image
- d’un tableau
- d’un graphique
Méthode
Le conseil est de maitriser par cœur le motif de la fonction linéaire : \( f(x)=ax \)
On voit que l’on a trois éléments: l’antécédent, x, le coefficient a, l’image f(x).
Si on en a 2, alors on a le troisième.
Pour déterminer le coefficient il suffit d’avoir un couple antécédent-image. Ce couple peut être donné directement ou lu sur un tableau ou un graphique.
Correction:
a)Déterminer l’expression d’une fonction à partir d’un couple antécédent-image:
\( f(3)=a \times 3= { 1 \over 2 } \rightarrow a={ 1 \over 6 } \newline f(x)={ 1 \over 6 } x \)
b) Déterminer l’expression d’une fonction à partir d’un couple lu sur un tableau:
\( g(7)=a \times 7=9 \rightarrow a={ 9 \over 7 } \Rightarrow g(x)={ 9 \over 7 } x \)
c) Déterminer l’expression d’une fonction à partir d’un couple lu sur un graphique:
On lit le point A({ 1 \over 2 } ;1)
\( k({ 1 \over 2 })=a \times { 1 \over 2 }=1 \Rightarrow a=2 \newline k(x)=2x \)
- Fonctions affines
Clé: Considérer la fonction affine comme la somme d’une fonction constante et d’une fonction linéaire
Intérêt: Les fonctions affines interviennent dans les tarifications dès qu’il y a abonnement, dès que pour 0, on n’a pas 0.
Méthode:
Trouver les paramètres de la fonctions nécessite deux couples antécédent-image car on a deux paramètres.
a)On considère la fonction : \( f(x)=3x-7 \)
Quelles sont les images de 0 et 2 ?
Quels sont les antécédents de 10 et -5 ?
b) Déterminer l’expression de la fonction affine f sachant que l’image de 3 est \( { 1 \over 2 } \) et celle de 0 est 2.
c) Déterminer l’expression de la fonction affine f sachant que l’image de 3 est 1/2 et celle de 5 est 2.
Intérêt
Le conseil est de maitriser par cœur le motif de la fonction affine : \( f(x)=ax+b \)
On voit que l’on a quatre éléments, l’antécédent, x, le coefficient a, l’image f(x) et l’ordonnée à l’origine b.
Méthode
Trouver les paramètres d’une fonction affine:
-Chercher la constante avec l’ordonnée à l’origine quand c’est possible (c’est le niveau 3ème)
-chercher le coefficient directeur avec un second couple d’informations une fois que l’on a la constante.
Correction:
a) Déterminer des images et des antécédents.
La recherche d’antécédent est toujours plus difficile.
En effet le calcul d’image est direct :
\( f(0)=0 \times 3-7=-7 \). L’image de 0 est -7.
\( f(2)=3×2-7=-1 \). L’image de 2 est -1.
Pour les antécédents il faut résoudre une équation :
\( f(x)=3x-7=10 \rightarrow 3x=17 \Rightarrow x={ 17 \over 3 } \)
L’antécédent de 10 est \( { 17 \over 3 } \).
\( f(x)=3x-7=-5 \Rightarrow 3x=2 \Rightarrow x={ 2 \over 3 } \)
L’antécédent de -5 est \( { 2 \over 3 } \)
b) et c) Déterminer l’expression d’une fonction affine
On a donc besoin de deux couples antécédents-images pour déterminer l’expression d’une fonction affine.
Ces deux couples peuvent être donnés ou lus sur un tableau ou un graphique.
a) Ce cas où on a l’ordonnée à l’origine est à maitriser en troisième.
L’ordonnée à l’origine permet d’obtenir b:
\( f(0)=a×0+b=2 \rightarrow b=2 \)
Le second couple \( ( 3; {1 \over 2 } ) \) permet d’obtenir a:
\(f(3)=a×3+2= {1 \over 2 } \Rightarrow 3a=-{3 \over 2} \Rightarrow a=-{1 \over 2} \)
On a donc : \( f(x)=-{1 \over 2} x+2 \)
b) Aucun des couples ne correspond à l’ordonnée à l’origine. Ce cas est difficile et c’est l’un des points les plus complexes de la troisième.
\( f(3)=a×3+b={1 \over 2} \newline f(5)=a×5+b=2 \)
Vous verrez l’année prochaine deux méthodes pour résoudre ce type de situation.
Une des méthodes est de soustraire les deux lignes pour que les « b » s’annulent.
\( f(5)-f(3)=5a-3a=2-{1 \over 2} \newline 2a={3 \over 2} \Rightarrow a={3 \over 4} \)
Ensuite on porte ce résultat dans l’une des deux lignes :
\( f(3)={3 \over 4} \times 3+b={1 \over 2} \newline b={1 \over 2} -{9 \over 4} =-{7 \over 4} \)
On a donc:
\( f(x)={3 \over 4} x-{7 \over 4} \)
Il n’est pas utile de voir les cas avec un tableau ou un graphique car ils reviennent au même : il nous faut deux couples, si un couple correspond à l’ordonnée à l’origine on est dans le cas simple, sinon c’est le cas complexe.
- Fonction affine: interprétation graphique
Clé: La représentation graphique de la fonction f est l’ensemble des points de coordonnées (x;f(x))
Intérêt: Les graphiques sont omniprésents dans notre vie quotidienne.
Méthode:
Pour une fonction affine on a besoin de deux points. Une droite est déterminée par deux points.
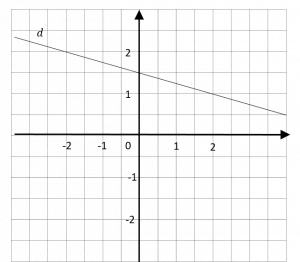
a) Quelle est l’image de 2 ? L’antécédent de 2 ?
b) La fonction f représentée par la droite d est de quel type ?
c) Quels en sont ses paramètres ?
Intérêt
L’évolution technologique est telle que la représentation graphique est de plus en plus privilégiée dans tous les domaines de la vie quotidienne.
La lecture graphique est donc une compétence à maitriser parfaitement. Image et antécédent ?
Identifier une fonction linéaire ou affine ?
Déterminer leurs paramètres ?
Méthode
Il faut comprendre que les fonctions du premier degré sont représentées par des droites.
Une droite est entièrement définie par deux points. En effet par deux points il ne passe qu’une droite.
La constante: il suffit de regarder l’ordonnée à l’origine. Ce seul point suffit car on sait qu’elle est parallèle à l’axe des abscisses.
Linéaire: comme elle passe par l’origine (premier point), il suffit d’un second point pour déterminer le coefficient directeur.
Affine: on a besoin de deux points.
Bien sur dès qu’on a l’ordonnée à l’origine, c’est plus facile.
Correction:
a) \( f(2)=1 \ et \ f(-2)=2 \)
b) La fonction f est représentée par une droite qui ne passe pas par l’origine, c’est donc une fonction affine:
\( f(x)=ax+b \)
c) Première méthode:
On doit déterminer a et b, donc on a besoin de deux points:
déterminer b: l’ordonnée à l’origine est \( { 3 \over 2 }:
\( f(0) = { 3 \over 2 } \Rightarrow f(0)=0 \times a +b = { 3 \over 2 } \newline \Rightarrow b= { 3 \over 2 } \)
déterminer a: on prend le point (2;1) ( c’est à nous de choisir celui que l’on veut, donc on essaie d’en prendre un facile).
\( f(2)=2 \times a + { 3 \over 2 } =1 \) On a placé la valeur de b que l’on a trouvée.
On résout l’équation d’inconnue a:
\( 2a=1 -{ 3 \over 2 } \Rightarrow a=-{ 1 \over 4 } \newline f(x)=-1/4 x+{ 3 \over 2 } \)
Seconde méthode :
Pour la comprendre il faut voir le cours.
Le principe est de s’affranchir de la constante et d’observer la partie proportionnelle.
On trouve le coefficient directeur: \( a={différence des images \over différence des antécédents} \)
\( a= \frac{f(2)-f(0)}{2-0}=\frac{1-\frac{3}{2}}{2}=-{ 1 \over 4 } \)
- Situation classique
Clé: Faire fonctionner le motif » \( f(x)=ax+b \) » pour avoir les trois cas possibles: \( a= 0 \ , \ b= 0 \ et \ a \neq 0 \ ,\ b \neq 0 \)
Intérêt: Il faut penser cette situation comme l’aboutissement du travail de modélisation du collège.
Méthode:
Comprendre les différentes tâches:
- identifier une fonction à partir de sa représentation
- déterminer la formule d’une fonction
- modéliser une situation par une fonction
- comparer des fonctions
- résoudre une équation
Les forfaits
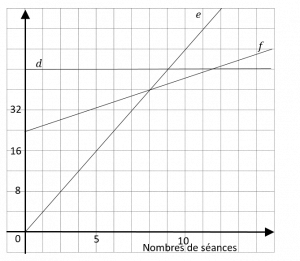
D est la représentation graphique de la fonction k, e celle de la fonction l, f celle de la fonction m.
a) Identifier le type de chacune des fonctions et justifier.
b) donner l’expression de chaque fonction.
Ces fonctions modélisent le prix pour n séances de natations dans une piscine qui offre trois tarifications différentes.
La première, A, est forfait illimité de 32€ par trimestre.
La seconde possibilité, B, est de payer chaque séance de natation à un prix donné.
La troisième tarification, C, propose un abonnement de 20€, et une réduction pour chaque séance.
c) A quelle fonction correspondent chacune des tarifications ?
d) A partir de combien de séances l’abonnement illimité est rentable.
e) Pour combien de séances les tarifs A et B sont égaux.
Intérêt
Dans la vie de tous les jours, il est essentiel de maîtriser le premier de gré pour les nombreuses choses que l’on entreprend ou les contraintes de la vie.
Méthode
Il n’y a que deux termes de de degré 1 ou inférieur: la contante et ax.
On a donc trois possibilités
– la constante
-le terme linéaire
-le terme linéaire plus la constante.
Correction:
a) Reconnaitre les représentations graphiques.
La droite d est parallèle à l’axe des origines, donc quelle que soit la valeur de x, l’image reste la même. L’image ne dépend donc pas de x, c’est fonction constante : \( k(x)=a \)
La droite e passe par l’origine donc c’est une fonction linéaire : \( l(x)=bx \)
La droite f ne passe pas par l’origine donc c’est une fonction affine: \( m(x)=cx+d \)
b) Déterminer l’expression d’une fonction
La droite d coupe l’axe des ordonnées en 32: \( k(x)=32 \)
Pour une fonction linéaire on a besoin que d’un point puisque la formule ne contient qu’un seul paramètre. On choisit le point A(8 ;28) qui appartient à la droite e.
On a donc :
\( l(8)=b \times 8=28 \Rightarrow b={ 28 \over 8 } = { 7 \over 2 } \newline l(x)={ 7 \over 2 } x \)
Pour une fonction affine on a besoin d deux points car la formule a deux paramètres. On choisit l’ordonnée à l’origine et le point A(8;28) qui appartient aussi à f.
La droite f coupe l’axe des ordonnées en 20. On a donc : \(m(0)=c \times 0+d=20 \Rightarrow d=20 \)
Cherchons le coefficient directeur:
Le point A(8 ;28) appartient aussi à f, donc :
\( m(8)=8c+20=28 \newline 8c=8 \Rightarrow c=1 \newline m(x)=x+20 \)
c) Modéliser une situation par une fonction
Le forfait illimité correspond à la fonction constante, en effet le prix ne dépend pas du nombre de séances.
La fonction linéaire correspond à la tarification B, chaque séance vaut le même prix.
La fonction affine correspond à la tarification C, l’ordonnée à l’origine étant l’abonnement.
d) Comparer des fonctions
Le tarif le plus avantageux est celui qui se trouve « en dessous » des autres. Jusqu’à 8 séances c’est le tarif proportionnel, puis celui avec abonnement, enfin au-delà de 12 séances c’est l’illimité.
e) Résoudre graphiquement une équation
On cherche le nombre de séances pour lequel les tarifs B et C sont égaux, c’est-à-dire lorsque les deux fonctions ont même image.
Les droites se coupent pour x=8.