Il faut être capable de trouver des antécédents et des images dans les trois représentations.
- Notion de fonction
Clé: Comprendre le schéma initial que relie les trois éléments: antécédent, image et fonction.
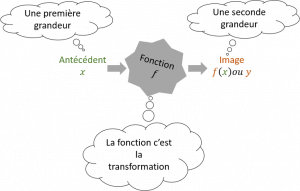
Intérêt:
Permettre de calculer une grandeur à partir d’une autre.
Méthode:
Une fonction peut être représentée par une formule, un tableau ou un graphique. Elle est aussi souvent définie par un programme de calcul car c’est ce qu’on utilise dans un tableur.
Pour chacune des représentations il faut maitriser :
-la définition de la fonction avec ses différentes écritures (voir cours)
-la recherche d’antécédents et d’images
Programme de calcul
Voici un programme de calcul
|
a) Que donne le programme si on choisit 0,1/3 ?
b) On a obtenu 20. Quel nombre a été choisi ?
On note f la fonction qui, au nombre choisi, associe le résultat obtenu.
c) Quelle est l’image de 3 ?
d) Quel est l’antécédent de 12?
Intérêt
C’est la situation la plus classique.
Méthode
Prendre l’habitude de toujours nommer un programme de calcul et de construire son expression littérale :
Correction:
Traduction du programme de calcul, c’est ce que l’on fait en 4ème et 5ème en calcul littéral:
\( P=(3x-1)4 \)
a) Pour x=0 ;P=-4
Pour \( x= { 1 \over 3 } ;P=0 \)
b) Se souvenir que la recherche d’un antécédent est toujours plus difficile. Trouver le point de départ est toujours plus dur que le point d’arrivée.
Deux méthodes :
« remonter le programme de calcul »
\( { 40 \over 4} =5; 5+1=6; {6 \over 3} =2 \)
« utiliser l’expression littérale »
\( (3x-1)4=20 \Rightarrow 12x-4=20 \)
x=2
c) La phrase doit être apprise par cœur. Vous devez absolument maitriser la syntaxe.
On définit la fonction f qui associe à tout nombre x le nombre f(x) :
\( f(x)=(3x-1)4 \newline f(3)=(3×3-1)4=32 \newline f(x)=(3x-1)4=12 \newline 12x-4=12 \Rightarrow 12x=16 \Rightarrow x= {16 \over 12 } = { 4 \over 3 } \)
Par le tableau
Ce tableau définit la fonction g qui associe à tout nombre x le nombre g(x).
| x | 3 | 1 | 2 | 8 |
| g(x) | 7 | 5 | 5 | 0 |
a) Quelle est l’image de 3 ? 8 ?
b) Quels sont les antécédents de 5 ?
c) On associe au nombre 1, g(1)=4. Est-ce possible ?
Intérêt
C’est la représentation qui permet de recueillir des informations.
Le tableau n’est opérationalisable que s’ii est de proportionnalité.
Méthode
Il suffit de bien identifier les antécédents et les images.
Correction
Le tableau est la représentation la plus facile. Il suffit de lire !
Les questions b et c sont pour rappelées qu’une image peut avoir plusieurs antécédents, mais qu’un antécédent ne peut avoir plusieurs images (souvenez-vous de l’objet lancé devant le tableau).
Par la formule
On considère les fonctions h et g qui associe à tout nombre x le nombre h(x) et g(x):
\( h:x \rightarrow 2x ;g:x \rightarrow 10-x \)
a) Quelle fonction associe à un nombre son double ?
b) Quelle est l’image de 10 par chacune des deux fonctions.
c) quel est l’antécédent de 9 par chacune des deux fonctions ?
d) On construit la fonction l qui associe à tout nombre x le nombre \( g(x)-h(x) \).
Ecrire l’expression de la fonction l.
Quelle est l’image par l de 3 ? Quel est l’antécédent de 5 ?
Intérêt
C’est la seule représentation qui permet de calculer des valeurs exactes (hors proportionnalité).
Le langage mathématique permet de modéliser les fonction à l’aide de ses lois.
Méthode
Toujours bien savoir ce que l’on écrit.
Correction:
a) C’est la fonction h qui associe à un nombre son double: \( hx) = 2x \)
\( h(10)=2 \times 10 = 20; g(10)=10-10=0 \newline h(x)=2x=9 \Rightarrow x= 4,5 \newline g(x)=10 – x =9 \Rightarrow x=19 \)
On définit la fonction l qui associe à tout nombre x le nombre \( g(x)-h(x) \)
\( l(x) = 10 – x -2x = 10 -3x \newline l(3)=10-33 \times 3 = 1 \newline l(x)= 10 -3x = 5 \Rightarrow -3x=-5 \Rightarrow x= \frac{5}{3} \)
Par le graphique
On considère la hauteur de deux objets suspendus, E et F, au-dessus d’un lit de bébé.
La hauteur zéro correspond à la hauteur des barreaux du lit. La fonction e est associée à l’objet E, et f à F.
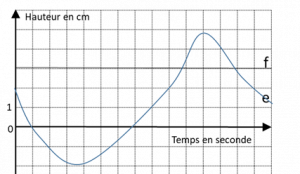
a) Identifier les deux fonctions.
b) Que peut-on dire du mobile F ?
c) Que peut-on dire du mobile E de 0s à 3s ? Et de 4s à 9s ?
d) Quels sont les antécédents de 0 par la fonction e ?
e) A quelle hauteur est le mobile E au bout de 10s ?
f) Quelle est l’image de 7 par la fonction e ?
g) Quand le mobile E est-il au-dessus du mobile F ?
Intérêt
Les mathématiques modernes et la facilité qu’offrent les moyens numériques pour réaliser des graphiques font que leur lecture est devenue indispensable.
Méthode
Correction:
Les tâches à maitriser sont :
– Etre capable de déterminer la fonction à partir des informations sur les axes (a)
La fonction e associe à tout temps en seconde la hauteur de l’objet E.
-être capable de déterminer des images et antécédents (d)(f)
Les antécédents de 0 :
Remarquez qu’une lecture graphique est forcément une approximation.
-être capable d’interpréter une évolution de la représentation graphique (b)(c)
L’objet F est à une hauteur constante, 3cm. On peut dire qu’il est immobile ( verticalement). De 0s à 3s l’objet E descend, puis remonte de 4s à 9s.
-être capable de comparer deux graphiques (g)
L’objet E est au-dessus de F lors sa représentation graphique est au-dessus : de 9,5s à 13s.