L’étude des nombres entiers au collège est structurée autour de la division euclidienne.
Remarques sur l'organisation mathématique du chapitre
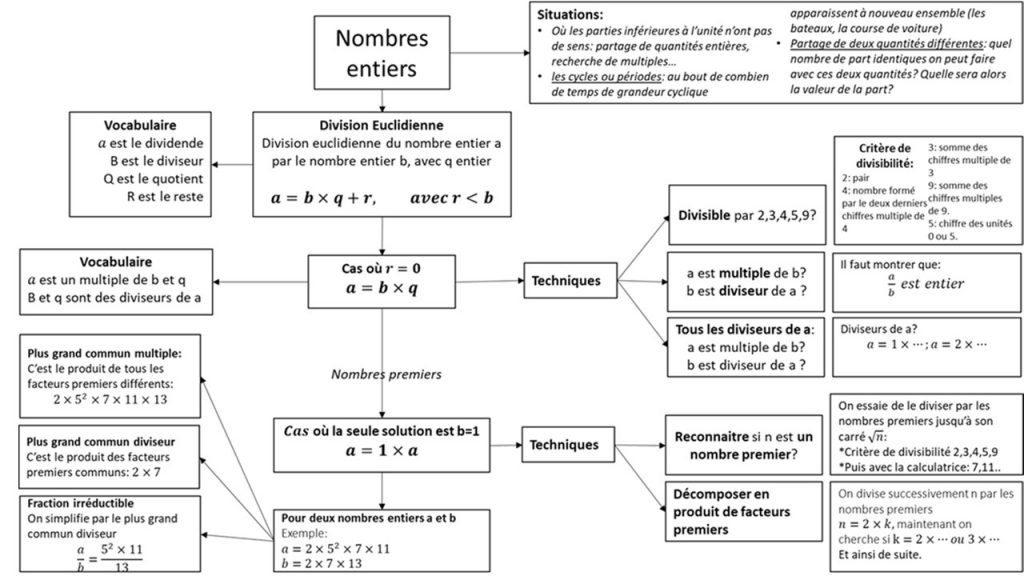
L’étude des nombres entiers au collège est l’étude de la division euclidienne et de ses cas particuliers.
Les techniques s’articulent autour de ces cas: multiples et diviseurs lorsque le reste est 0, nombres premiers lorsque q=1.
On peut considérer que ce chapitre est l’optimisation technique pour trouver des multiples et de diviseurs.
Démonstration du chapitre
Critère de divisibilité:
Par 3 et 9: Considérons un nombre entier n dont les chiffres des unités, des dizaines et des centaines sont c, d et u.
\( n = 100c+10d+u \newline =99 c+9d + (c+d+u) \newline =9(11 c+d) + (c+d+u) \)
le terme 9(11c+d) est divisible par 3 et 9. Le nombre n sera divisible par 3 et 9 si c+d+u est divisible par 3 et 9.
Par 4: considérons un nombre entier n avec d,u les chiffres des dizaines et unités.
\( n= k \times 100 + 10d +c \) avec k entier.
\( 100k= 4 \times 25 \times k \)
Donc est divisible par 4.
n sera divisible par 4 si 10d+u l’est.