La leçon sera réussie si vous avez compris que l’étude des nombres entiers revient à celle de la division euclidienne et de ses cas particuliers.
Il faut avoir retenu:
*le motif de la division euclidienne
*multiples et diviseurs
*critère de divisibilité
*nombre premier
*plus grand diviseur commun et plus petit multiple commun
Il faut être capable de:
* partager un nombre entier ave la division euclidienne
* trouver des multiples et diviseurs d’un nombre
* reconnaitre un nombre premier
* décomposer un nombre premier en produit de facteurs premiers
* trouver le plus grand diviseur commun et le plus petit multiple commun de deux nombres entiers.
La grande question qui structure l’apprentissage des nombres entiers au collège est :
« Comment peut-on partager un nombre entier en des nombres entiers ? »
En effet les situations faisant intervenir les additions, les soustractions et multiplications ne posent pas de problèmes, les sommes, différences et produits seront entiers.
Mais qu’en est-il lorsqu’on partage ?
Le cœur du chapitre est l’outil de partage des nombres entiers : la division euclidienne et ses cas particuliers:
* si r=0, on parle de multiples et diviseurs
* si r=0 et q=1, on parle de nombres premiers.
Division euclidienne
Définition
Effectuer la division euclidienne d’un nombre entier a (le dividende) par un nombre entier b (le diviseur) différent de 0, c’est trouver deux nombres entiers, le quotient q et le reste r tels que :
$$ a=q \times b + r \ avec \ r<b$$
Exemple
\( 185 = 26 \times 7 + 3 \ et \ 3 < 7 \). Le quotient est 26 et le reste 3.
Premier cas particulier de la division euclidienne: r=0.
Multiples et diviseurs d'un nombre
Définition
Un nombre entier a est un multiple d’un nombre entier b (b≠0) lorsque le reste de la division euclidienne de a par b est 0.
On dit aussi que b est un diviseur de a ou que a est divisible par b
Exemple
105 est un multiple de 1 car \( 105=7 \times 15 \);
15 est un diviseur de 105 car \( 105 \div 15 =7 \ et \ 7 \ est \ entier. \)
Il faut absolument les connaitre par coeur.
Critère de divisibilité
Propriétés
Un nombre entier est divisible par : | |
2 | Lorsque son chiffre des unités est 0, 2, 4, 6, 8 |
3 | Lorsque la somme de ses chiffres est divisible par 3 |
4 | Lorsque le nombre formé par ses deux derniers chiffres est divisible par 4 |
5 | Lorsque son chiffre des unités est 0 ou 5 |
9 | Lorsque la somme de ses chiffres est divisible par 9 |
10 | Lorsque son chiffre des unités est 0 |
Exemple
*2160 est divisible par 2, 5, 10. En effet le chiffre des unités est 0.
*2160 est divisible par 4. En effet, 60 est divisible par 4 (\(4 \times 15 \) )
*2160 est divisible par 3 et 9. En effet, \( 2+1+6+0=9 \) et 9 est divisible par 3 et 9.
La catégorisation permet de comprendre tous les situations différentes.
Division euclidienne: catégorisation des situations
Catégorisation
| $$ a=b \times q + r $$ | ||||
Cas où \( r \neq 0 \) $$ a=b \times q + r $$ | Cas où \( r=0 \) $$ a= b \times q $$ | |||
| Dividende ? | Quotient ou diviseur ? | Reste ? | a multiple de b ? $$ \frac{a}{b}=q$$ q est-il entier ou pas ? | b diviseur de a ? $$ \frac{a}{b}=q$$ q est-il entier ou pas ? |
On peut calculer la division euclidienne de a par b ou Connaissant trois nombres on peut trouver le quatrième | ||||
Exemple
* On veut faire des 84 boites de 18 chocolats et en garder 12 pour soi. On a le quotient 84, le diviseur 18, le reste 12. On cherche le dividende.
* On veut faire des boites de 6 chocolats avec 50 chocolats. On a le dividende et le diviseur, on cherche le quotient et le reste.
Multiples et diviseurs?
13 diviseur de 91 ? Cela revient à chercher si \( \frac{91}{13} \) est entier.
Remarquez que chercher si 91 est un multiple de 13 revient à la même chose, chercher si \( \frac{91}{13} \) est entier.
Second cas particulier: r=0 et q=1
Nombres premiers
Définition
Un nombre premier est un entier naturel qui admet exactement deux diviseurs: 1 et lui-même.
Exemple
*15 n’est pas premier car il est divisible par 3 et 5. On peut écrire 15 sous la forme de différents produits: \( 15=3 \times 5=15 \times 1 \).
*17 est premier car il n’est divisible que par 1 et 17. La seule solution pour écrire 17 sous la forme d’un produit est \( 17=17 \times 1 \).
Méthode
Méthode: reconnaitre un nombre premier
Exemples : 147 et 223 sont-ils premiers ?
147: En utilisant les critères de divisibilité on trouve que 147 est divisible par 3.
Donc il n’est pas premier.
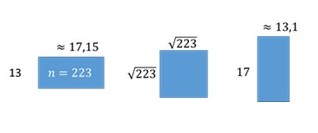
223: Aucun critère ne marche. Il va donc falloir utiliser la calculatrice et diviser par les différents nombres premiers jusqu’à la racine carrée du nombre cherché (voir remarque) : \( \sqrt{223} \simeq 14,9 \).
Si on obtient un nombre entier alors le nombre n’est pas premier.
\( 223 \div 7 \simeq 31,8; 223 \div 11 \simeq 20,2 ; 223 \div 13 \simeq 17,1 \)
Donc 223 est un nombre premier.
Remarque pour comprendre la méthode:
On restreint la recherche jusqu’à la racine carrée du nombre car un produit est l’aire d’un rectangle de dimension a et b par exemple et on a,
$$ a \times b = b \times a $$
Il est donc inutile de chercher au-delà du carré car on obtiendrait les mêmes rectangles retournés.
Propriété (admise)
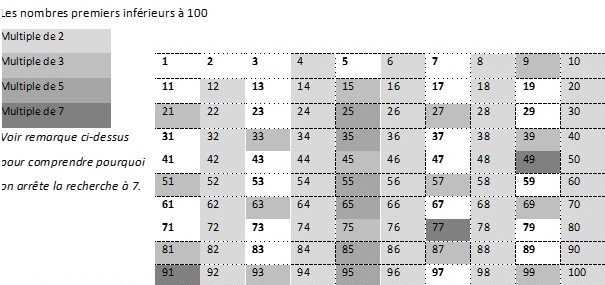
Il existe une infinité de nombres premiers.
Il est recommandé de connaitre les nombres premiers inférieurs à 100.
Décomposer un entier en produit de facteurs premiers
Propriété (admise)
n désigne un entier supérieur ou égal à 2.
n peut s’écrire comme un produit de nombres premiers, c’est à dire sous la forme:
\( n= p_{1}^{k_1} \times p_{2}^{k_2} \times … \)
où \( p_1, p_2 \) sont des nombres premiers et \( k_1, k_2 \) des entiers naturels.
Cette écriture est appelée décomposition en facteurs premiers de n.
Méthode
La méthode consiste à diviser par le premier nombre premier, 2, puis de recommencer avec le quotient obtenu par 2 et les nombres premiers suivants jusqu’à obtenir un nombre premier.
On vous propose deux présentations différentes.

Propriété (admise)
Pour un entier donné, il n’existe qu’une seule décomposition en produit de facteurs premiers (si l’on ne tient pas compte de l’ordre des facteurs).
Cas de deux nombres premiers
Définition: Fraction irréductible.
Une fraction est dite irréductible lorsque le numérateur et le dénominateur n’ont pas d’autre diviseur commun que 1.
Méthode: rendre une fraction irréductible
Exemple: \( \frac{84}{30} \)
On cherche le plus grand diviseur commun (voir ci-dessous):
\( 84 = 2^2 \times 3 \times 7 \ et \ 30 = 2 \times 3 \times 5 \)
Le plus grand diviseur commun est \( 2 \times 3 \):
\( \frac{84}{30}= \frac{84 \div 6 }{30 \div 6 }=\frac{14}{5} \)
Lorsque on a deux nombres entiers on peut définir deux nombres particuliers:
Définition. Plus petit commun multiple Soit deux nombres entiers a et b, le plus petit multiple commun est le nombre entier le plus petit qui soit à la fois multiple de a et de b. | Définition. Plus grand commun diviseur Soit deux nombres entiers, le plus grand diviseur commun est le diviseur le plus grand parmi l’ensemble des diviseurs communs des deux entiers. |
Une méthode pour trouver ces deux nombres est d’effectuer les décompositions en facteur premier:
$$ 1170= 2 \times 3^2 \times 5 \times 13 $$
$$ 1320= 2^3 \times 3 \times 5 \times 11 $$
- Le plus grand diviseur commun est le produit des diviseurs communs: $$2 \times 3 \times 5=30$$.
- Le plus petit multiple commun est le produit de tous les facteurs: $$ 13 \times 3 \times 30 \times 2^2 \times 11=51480 $$
On lit ces deux nombres facilement sur la représentation ci-dessous.
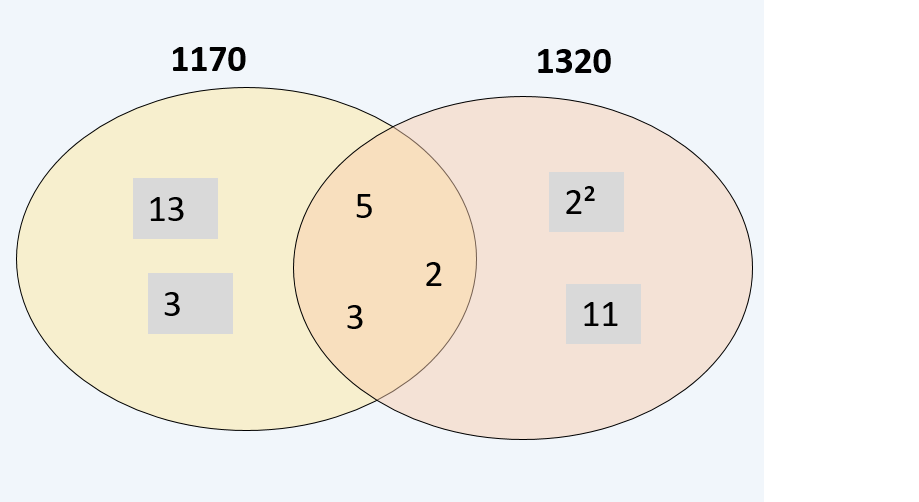
Cette représentation permet de résoudre les deux situations classiques suivantes:
Partage de deux quantités
On a 1170 bonbons et 1320 sucettes. On veut faire le plus de sachets possible identiques en utilisant tout les bonbons et toutes les sucettes.
Remarque: La difficulté est que l’on a ni le nombre de parts ni la valeur de la part.
On cherche le plus grand diviseur commun d:
$$d = 3 \times 2 \times 5 = 30 $$
On peut donc faire 30 sachets de 39 bonbons et 44 sucettes.
Situations de cycles (ou périodes)
Deux voitures partent en même temps et tournent autour d’un circuit. L’une, A, tourne en 1170s et l’autre, B, en 1320s. Au bout de combien de temps se retrouveront-elles en même temps sur la ligne de départ?
Ce temps t doit être le plus petit multiple commun.
On sait que $$ t = 1170 \times n_{tours \ de \ A}$$ et $$ t = 1320\times n_{tours \ de \ B}$$
$$ t= \overbrace{3 \times 13 \times 3 \times 2 \times 5}^{1170 \ temps de A} \underbrace{\times 2^2 \times 11}_{nombre \ de \ tour \ de \ A} $$
mais aussi,
$$ t= \underbrace{3 \times 13}_{nombre \ de \ tour \ de \ B} \overbrace{\times 3 \times 2 \times 5 \times 2^2 \times 11}^{1320\ temps de B} $$